場ごとの目的とは（トイツ場概論4）

ご存知のとおり（？）麻雀の場はランダムなパラレルワールドの集合体として存在する…と思われてきました。しかしドイツの数学者ゲオルク・フリードリヒ・ベルンハルト・リーマンは、ゼータ関数の解がゼロになる点を4つ求め、それらが一直線上に存在することを発見しました。そして「ゼータ関数の非自明なゼロ点はすべて一直線上にあるはずだ」という、リーマン予想を1859年に発表しました。

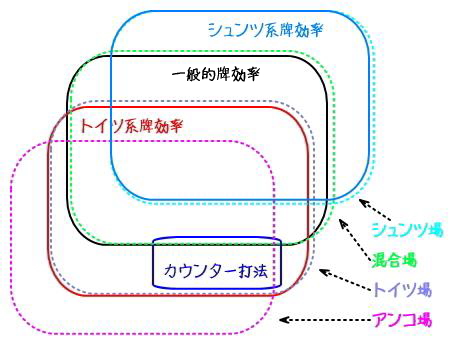
リーマンが求めたこの4つの点こそが「シュンツ系牌効率」「一般的牌効率」「トイツ系牌効率」「アンコ（コーツ）系牌効率」…だったとかそうでないとか…

これら4つの点のうち「シュンツ系牌効率」と「一般的牌効率」は、古今東西の数学者（？）によってほぼ正確に求められております。

そして問題の「トイツ系牌効率」は桜井章一氏と土田浩翔氏による「トイツ場は筋牌が重なる」という「桜井・土田予想」が発表されましたが、これはトイツ場の1つの傾向を証明したに過ぎず、この方向での解明に行き詰まりが指摘されていました。しかし現在私が研究中で、その全貌がかなりのところまで解明されています。

「アンコ（コーツ）系牌効率」については、先述の土田氏によって書かれた文献が見つかっていますが、残念ながら不完全なものであると言わざるを得ません。麻雀上の未解決問題のひとつであり、クレイ麻雀研究所はミレニアム懸賞問題の1つとして解決者に対して100万ドルの懸賞金を支払うことが約束されています。

まずは、よく知られている「一般的牌効率」からです。「一般的牌効率」は単に和了ることが目的です。麻雀の和了は2種類、つまり出和了とツモ和了がありますが、「一般的牌効率」ではそのこだわりはありません。そして和了という目的のための手段として広い聴牌、広い一向聴、広い二向聴・・・を目指しますが、その根拠となるのは「自分の手牌」です。ベースの役は、タンヤオ・役牌・（平和）です

では「シュンツ系牌効率」はどうでしょう？　もちろん和了ることが目的になりますが、「シュンツ系牌効率」は出和了目的です。その目的のための手段として行うのが迷彩です。そしてそのために根拠とするのが「自分の捨て牌」です。ベースの役は、三色・一通・チャンタ・（平和）です。

そこから見える「トイツ系牌効率」の姿ですが、和了ることが目的なのは変わりありません。しかし私の研究から「トイツ系牌効率」はツモ和了重視と分かっています。出和了は保険になります。そのために根拠とするのは「相手の捨て牌」になります。そしてそこから発展させて「相手の手牌」、さらに「山牌」もその対象となるのではないかと予想されています。ベースの役は、七対子（チートイツ）です。

「トイツ系牌効率」すら完全に解明されていない現在、「アンコ（コーツ）系牌効率」については多くを語ることはしないでおこうと思っていました。しかしせっかくなので軽く触れておきましょう。

和了について言えば先ほどのリーマン予想（？）を信じるなら「ツモ和了目的」になるのではないかと考えるでしょう。しかしこれが罠なのです。多くの学者たちが「シュンツ場→混合場→トイツ場→アンコ（コーツ）場」が2次元の一直線だと考えていたのですが、私の考えとしては3次元での一直線だったのです。

イメージとしては「球」の表面に描かれた直線がそれです。それは2次元視点で考えると円になります。つまり「アンコ（コーツ）場」の向こう側は壁になっているのではなく、ぐるっと回って「シュンツ場」になっている可能性があるということです。

それが未開の地である「アンコ（コーツ）場」の秘密、そして麻雀の不条理を解き明かす鍵になると私は考えるのですが、今はそれ以前に「トイツ系牌効率」の解明が先ですので、「アンコ（コーツ）場」や「アンコ（コーツ）系牌効率」についてはこの程度で置いておきましょう。